Personal homepage of Matthias Liero

I am a post-doc at the Weierstraß Institute for Applied Analysis and Stochastics, Berlin, in the research group Partial Differential Equations of Alexander Mielke. I am also a member of the Berlin Mathematical School (BMS) in the Postdoctoral Faculty.

Contact

• Weierstraß-Institut, Mohrenstraße 39, 10117 Berlin, Office 303

• E-mail: Matthias.Liero-please-remove-this-text-@wias-berlin.de, (Public Key)

• Phone: +49 (0) 30 20372 542

• Fax: +49 (0) 30 20372 311

• ORCID: 0000-0002-0963-2915

Research interests

My mathematical expertise is in the field of nonlinear partial differential equations. In particular, the rigorous derivation of new effective models in various problems in natural sciences using novel mathematical techniques is one of my major interests. In my diploma I gave a rigorous justification of an evolutionary elastoplastic plate model for continuum mechanics using the notion of Gamma-convergence. In a joint work with U. Stefanelli (Vienna), we extended the Weighted-Energy-Dissipation principle from parabolic to hyperbolic equations to make them accessible to variational methods.

In the recent years, the mathematical modeling, analysis, and simulation of optoelectronic devices, such as solar cells and organic light-emitting diodes, has become an essential application for me. I work closely with my colleagues A. Glitzky, Th. Koprucki, J. Fuhrmann, and D.H. Doan from WIAS on organic devices.

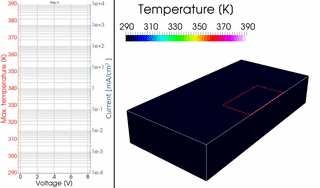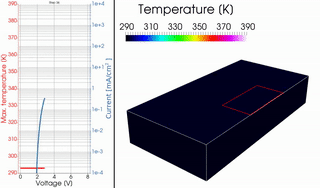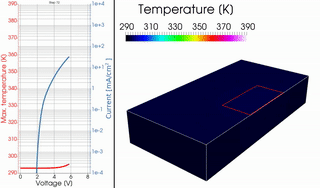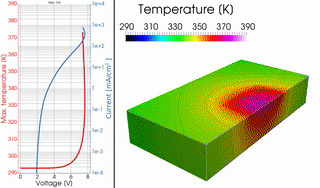
In a joint work with the Dresden Integrated Center for Applied Physics and Photonic Materials, in particular with A. Fischer, R. Scholz and S. Reineke, we derived a novel PDE model, involving the p(x)-Laplacian with discontinuous p(x), to describe the current and heat flow in organic light-emitting diodes. This was the first model to correctly predict S-shaped current-voltage characteristics with regions of negative differential resistance as observed in measurements.

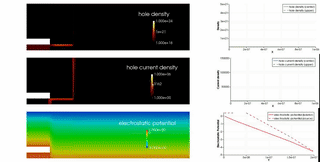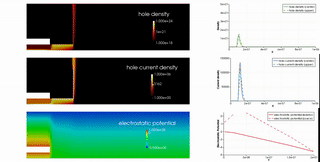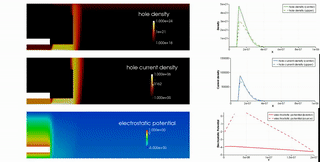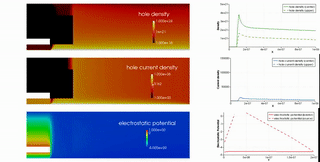
Moreover, with M. Sawatzki and H. Kleemann from IAPP we investigate the behavior and new concepts of organic transistors.

However, also the more abstract theory behind partial differential equations is in the focus of my current work. One particular highlight of a recent joint work with A. Mielke (WIAS & HUB) and G. Savaré (Milano) was the derivation and characterization of the so-called Hellinger-Kantorovich distance, which can be seen as a generalization of the famous Wasserstein distance to arbitrary measures.

In general, my scientific work is guided by the aim to strengthen the cooperation between analysis and its applications by inventing and further developing the mathematical foundations and techniques to make them applicable for practical questions in other sciences.

I am contributing to the software projects pdelib, ddfermi, VoronoiFVM.jl, ExtendableGrids.jl.

Current projects

• MATH+ subproject AA2-10, Electro-Mechanical Coupling for Semiconductor Devices, with Patricio Farrell (WIAS), A. Glitzky (WIAS), and Barbara Zwicknagl (HUB), January 2021 – December 2022

• SPP 2256 Varational Methods for Predicting Complex Phenomena in Engineering Structures and Materials, subproject Analysis for thermo-mechanical models with internal variables, with A. Mielke (WIAS & HUB), 2021 – 2023

Completed projects

• ECMath subproject SE18 in Research Center Matheon, Models for heat and charge-carrier flow in organic electronics, with A. Glitzky (WIAS), June 2017 – December 2018

• MATH+ transition project SE18, Models for heat and charge-carrier flow in organic electronics, with A. Glitzky (WIAS), January 2019 – September 2019

• MATH+ subproject AA2-1, Hybrid models for the electrothermal behavior of organic semiconductor devices, with A. Glitzky (WIAS), January 2019 – December 2020

Teaching

• summer term 2021: Partial Differential Equations, at Humboldt Universität zu Berlin, Wednesday from 9am and Thursdays from 11:30 am. The tutorial is on Thursday from 1:30pm

• summer term 2018: Multidimensional Calculus of Variations, at Humboldt Universität zu Berlin, Tuesdays from 1pm and Thursdays from 9am. The tutorial is on Tuesday from 3pm

• winter term WS2017/18: Optimal transport and Wasserstein gradient flows, at Humboldt Universität zu Berlin, Tuesdays from 9am

See teaching page for more details.

Publications

1. A. Kirch, A. Fischer, M. Liero, J. Fuhrmann, A. Glitzky, S. Reineke. Electrothermal tristability causes sudden burn-in phenomena in organic LEDs, accepted for publication in Adv. Funct. Mater., 2021 (Link)

2. A. Glitzky, M. Liero, G. Nika. A coarse-grained electrothermal model for organic semiconductor devices, WIAS Preprint 2822, 2021

3. A. Glitzky, M. Liero, G. Nika. Dimension reduction of thermistor models for large-area organic light-emitting diodes, Discr. Cont. Dynam. Systems Ser. S, 14:11, pp. 3953–3971, 2021 (Link)

4. A. Glitzky, M. Liero, Grigor Nika. An existence result for a class of electrothermal drift-diffusion models with Gauss–Fermi statistics for organic semiconductor devices, Analysis and Applications, 19(02), pp. 275-304, 2021 (Link)

5. Th. Frenzel, M. Liero. Effective diffusion in thin structures via generalized gradient systems and EDP-convergence, Discr. Cont. Dynam. Systems Ser. S, 14(1), pp. 395–425, 2021 (Link)

6. A. Glitzky, M. Liero, G. Nika. Analysis of a bulk-surface thermistor model for large-area organic LEDs, Portugaliae Mathematica, 78:2, pp. 187–210., 2020 (Link)

7. A. Glitzky, M. Liero, G. Nika. A hybrid model for the electrothermal behavior of semiconductor devices, PAMM Proc. Appl. Mech., DOI 10.1002/pamm.202000028, 2020

8. D. H. Doan, A. Fischer, J. Fuhrmann, A. Glitzky, M. Liero. Drift-diffusion simulation of S-shaped current-voltage relations for organic semiconductor devices, Journal of Computational Electronic, 19:3 pp. 1164–1174, 2020 (Link)

9. S. Reineke, A. Kirch, A. Fischer, M. Liero, J. Fuhrmann, A. Glitzky. Experimental proof of Joule heating-induced switched-back regions in OLEDs, Light: Science & Applications, 9, 5, 2020 (Link)

10. J. Fuhrmann, D. H. Doan, A. Glitzky, M. Liero, G. Nika. Unipolar drift-diffusion simulation of S-shaped current-voltage relations for organic semiconductor devices, in: R. Klöfkorn, E.Keilegavlen, F. Radu, J. Fuhrmann (eds) Finite Volumes for Complex Applications IX - Methods, Theoretical Aspects, Examples: FVCA 9, Bergen, Norway, Springer Proceedings in Mathematics & Statistics, vol. 323. Springer, Cham, pp. 625–633, 2019

11. A. Glitzky, M. Liero, G. Nika. Analysis of a hybrid model for the electro-thermal behavior of semiconductor heterostructures, accepted for publication in Journal of Mathematical Analysis and Applications, WIAS Preprint 2636, 2019

12. A. Glitzky, M. Liero. Instationary drift-diffusion problems with Gauss–Fermi statistics and field-dependent mobility for organic semiconductor devices, Comm. Math. Sci., 17, 33–59, 2019 (Link)

13. D. H. Doan, A. Glitzky, M. Liero. Analysis of a drift-diffusion model for organic semiconductor devices, Z. Angew. Math. Phys., 70, 55, 2019 (Link)

14. M. Liero, S. Melchionna. The weighted energy-dissipation principle and evolutionary $\Gamma$-convergence for doubly nonlinear problems, ESAIM Control Optim. Calc. Var., 25, 36, 2019, (Link)

15. Y. Zheng, A. Fischer, M. Sawatzki, D. H. Doan, M. Liero, A. Glitzky, S. Reineke, Stefan C. B. Mannsfeld. Introducing pinMOS Memory: A Novel, Nonvolatile Organic Memory Device, Advanced Functional Materials, 1907119, 2019 (Link)

16. K. Disser, M. Liero, Jonathan Zinsl. Evolutionary $\Gamma$-convergence of gradient systems modeling slow and fast chemical reactions, Nonlinearity, 31, 3689–3706, 2018 (Link)

17. M. Liero, A. Mielke, G. Savaré. Optimal Entropy-Transport problems and a new Hellinger–Kantorovich distance between positive measures, Inventiones mathematicae, 211, 969–1117, 2018 (Link)

18. F. M. Sawatzki, D. H. Doan, H. Kleemann, M. Liero, A. Glitzky, Th. Koprucki, K. Leo. Balance of Horizontal and Vertical Charge Transport in Organic Field-Effect Transistors, Phys. Rev. Applied, 10, 034069, 2018 (Link)

19. A. Fischer, M. Pfalz, K. Vandewal, S. Lenk, M. Liero, A. Glitzky, S. Reineke. Full Electrothermal OLED Model Including Nonlinear Self-heating Effects, Phys. Rev. Applied, 10, 014023, 2018 (Link)

20. M. Liero, S. Reichelt. Homogenization of Cahn–Hilliard-type equations via evolutionary $\Gamma$-convergence, Nonlinear Differential Equations and Applications NoDEA, 25, 6, 2018, (Link)

21. J. Fuhrmann, A. Glitzky, M. Liero. Hybrid Finite-Volume/Finite-Element Schemes for p(x)-Laplace Thermistor Models, In: Clément Cancès, Pascal Omnes (eds.) Finite Volumes for Complex Applications VIII - Hyperbolic, Elliptic and Parabolic Problems: FVCA 8, Lille, France, June 2017, 397–405, 2017

22. M. Liero, J. Fuhrmann, A. Glitzky, Th. Koprucki, A. Fischer, S. Reineke. 3D electrothermal simulations of organic LEDs showing negative differential resistance, Opt. Quantum Electron., 49, 330/1–330/8, 2017 (Link)

23. Miroslav Bulíček, A. Glitzky, M. Liero. Thermistor systems of p(x)-Laplace-type with discontinuous exponents via entropy solutions, Discr. Cont. Dynam. Systems Ser. S, 10, 697–713, 2017 (Link)

24. M. Liero, A. Mielke, Mark A. Peletier, D. R. Michiel Renger. On microscopic origins of generalized gradient structures, Discr. Cont. Dynam. Systems Ser. S, 10, 1, 2017, (Link)

25. A. Glitzky, M. Liero. Analysis of p(x)-Laplace thermistor models describing the electrothermal behavior of organic semiconductor devices, Nonlinear Analysis: Real World Applications, 34, 536–562, 2017, (Link)

26. M. Liero, A. Fischer, J. Fuhrmann, Th. Koprucki, A. Glitzky. A PDE Model for Electrothermal Feedback in Organic Semiconductor Devices, Progress in Industrial Mathematics at ECMI 2016, 99–106, 2017

27. M. Liero, J. Fuhrmann, A. Glitzky, Th. Koprucki, A. Fischer, S. Reineke. Modeling and Simulation of Electrothermal Feedback in Large-area Organic LEDs, Proceedings of the 17th International Conference on Numerical Simulation of Optoelectronic Devices, NUSOD 2017, 105–106, 2017

28. M. Liero, The Hellinger-Kantorovich distance as a generalization of optimal-transport distances to scalar reaction-diffusion problems, Oberwolfach Rep. 14, 47–50, 2017

29. M. Bulíček, A. Glitzky, M. Liero. Systems describing electrothermal effects with p(x)-Laplace like structure for discontinuous variable exponents, SIAM J. Math. Analysis, 48, 3496–3514, 2016 (Link)

30. A. Bercegol, B. Chacko, R. Klenk, I. Lauermann, M. Ch. Lux-Steiner, M. Liero. Point contacts at the copper-indium-gallium-selenide interface–A theoretical outlook, Journal of Applied Physics, 119, 155304, 2016, (Link)

31. M. Liero, A. Mielke, G. Savaré. Optimal Transport in Competition with Reaction: The Hellinger–Kantorovich Distance and Geodesic Curves, SIAM Journal on Mathematical Analysis, 48, 2869–2911, 2016, (Link)

32. M. Liero, Th. Koprucki, A. Fischer, R. Scholz, A. Glitzky, p-Laplace thermistor modeling of electrothermal feedback in organic semiconductor devices, Z. Angew. Math. Phys., 66, 2957–2977, 2015 (Link)

33. K. Disser, M. Liero. On gradient structures for Markov chains and the passage to Wasserstein gradient flows, Networks & Heterogeneous Media, 10, 233–253, 2015, (Link)

34. M. Liero, A. Mielke. Gradient structures and geodesic convexity for reaction-diffusion systems, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 371, 20120346, 2013, (Link)

35. M. Liero. Passing from bulk to bulk-surface evolution in the Allen–Cahn equation, Nonlinear Differential Equations and Applications NoDEA, 20, 919–942, 2013, (Link)

36. M. Liero, U. Stefanelli. A new minimum principle for Lagrangian mechanics, J. Nonlinear Sci., 23, 179–204, 2013 (Link)

37. M. Liero, U. Stefanelli. Weighted inertia-dissipation-energy functionals for semilinear equations, Boll. Unione Mat. Ital. (9), 6, 1–27, 2013 (Link)

38. M. Liero, Th. Roche. Rigorous derivation of a plate theory in linear elastoplasticity via $\Gamma$-convergence, Nonlinear Differential Equations and Applications NoDEA, 19, 437–457, 2012, (Link)

39. M. Liero, A. Mielke. An evolutionary elastoplastic plate model derived via $\Gamma$-convergence, Math. Models Meth. Appl. Sci. (M$^3$AS), 21, 1961–1986, 2011 (Link)

40. Pavel Krejčí, M. Liero. Rate independent Kurzweil processes, Applications of Mathematics, 54, 117–145, 2009, (Link)

41. H. Liero, M. Liero. Testing the Acceleration Function in Lifetime Models, In: Filia Vonta, Mikhail Nikulin, Nikolaos Limnios, Catherine Huber-Carol (eds.) Statistical Models and Methods for Biomedical and Technical Systems, 225–239, 2008, (Link)